Belt pulley mechanisms are systems commonly found in various businesses. They are used to transmit rotational motion generated by one mechanism to another, and they can also change the power or speed of rotation.

Advantages:

• They have the ability to operate over a wide range of speeds.
• Belts do not require lubrication.
• They are cheaper than chains for low power and low-speed applications.
• Flat belts are the best mechanism for high-speed transmissions.
• Belts can slip under excessive loads, providing a protective function in preventing mechanical damage on shafts.
• They provide a suitable solution for long distances between axes.
• They can operate in open environments as they do not require lubrication.

Disadvantages:

• They are not suitable for precise timing tasks, except for timing belts, as slippage can occur.
• Belts can be affected by chemicals and temperature.
• They can create vibrations, operate noisily, and produce noise in case of any issues.

Things to Consider in the Assembly of Belt-Pulley Systems:

• Belt should not sink more than 1mm into the pulley groove compared to the initial assembly for V-belts.
• The belt should not exceed 60°C under normal operating conditions.
• There should be no abrasive substances, grease, or oil vapor in the working area (contact area).
• Regular tension checks of belts are necessary.
• Pulleys should undergo a balancing process after production.
• Care should be taken to avoid impacts on the pulleys during assembly.
• Belts should never be forced with tools like levers or screwdrivers during installation.

Basic Parameters in Belt-Pulley Systems:

Flat Belts:

The moment that flat belts can transmit is calculated as in band brakes:

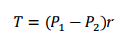
Intermediate processes can be added from the band brakes section.

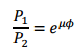
Here, P1 is the tight side and P2 is the slack side belt tension, µ is the friction coefficient, and ф is the total contact angle of the belt on the pulley. The required belt tension Pi depends on the elastic properties of the belt and is usually calculated as follows:

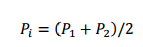
Assuming that the belt-pulley system moves slowly enough, inertial forces of the belt can be neglected. Since belts usually move quite rapidly during power transmission, they are also affected by centrifugal forces. The belt experiences a force Pc as a result of the centrifugal force. The resulting Pc force is expressed as follows:

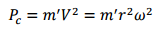
Here:

mL: Mass of the belt per unit length

V: Linear velocity of the belt

r: Pulley radius

The Pc force must be added to the equations above. Accordingly, the new equation is expressed as follows:

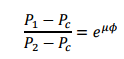
V-Belts:

 

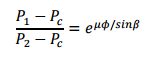
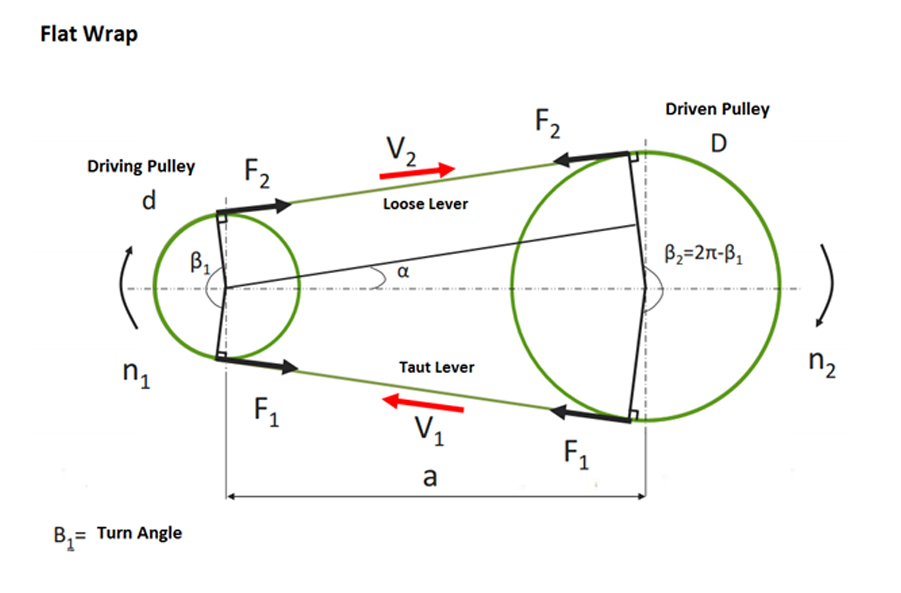
Size	Formula
Wrapping Angle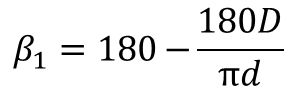
Belt Length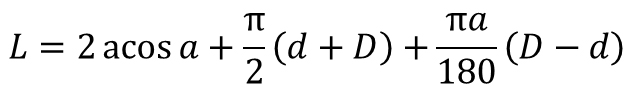
Belt Length (practical)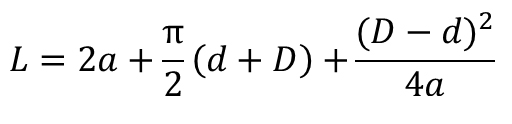
Pulley Diameter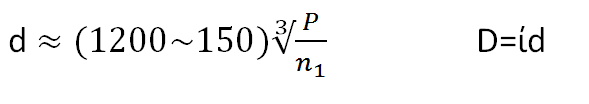
Belt Inclination Angle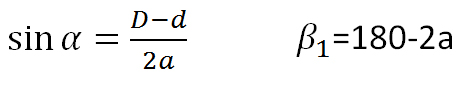

Problem:

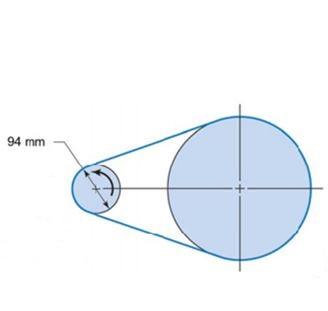
The electric motor drives a 19kW machine part at 1750rpm using multiple V-belts. Size is 5V-belt β = 18 ° and the unit mass of the belt is 0.215gr / mm. The pitch diameter of the motor pulley is 94 mm and the wrapping angle of the belt is 165 °.

Calculate how many V-belts are to be used, assuming that the tension load in the belt is maximum 672 N and the friction coefficient is 0.20.

Given:

Power: 19 kW, rotation speed 1750 rpm, belt type, β = 18, unit weight = 0.215 gr / mm, Pulley diameter = 94 mm,ф = 165, Pmax = 672N and ɥ = 0.20

Solution:

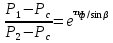 ve T=r

P_c is not known here.

 

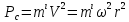
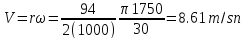
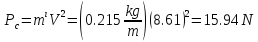
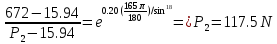
T=(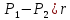=(672-117.5)(94/(2x1000))=26.1 Nm

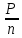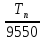T=9550=> P===4.78 kW/kayış

Number of Belts =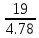=3.97 belts, and the number of belts is  4.

 

Taper Bushing Tightening Table

Suggested Key Torque Values for Tightening Taper Bush
Bushing No	Screw Tightening Torque (Nm)
1008	5,6
1108	5,6
1210	20,0
1215	20,0
1310	20,0
1610	20,0
1615	20,0
2012	30,0
2517	50,0
2525	50,0
3020	90,0
3030	90,0
3525	115,0
3535	115,0
4030	170,0
4040	170,0
4535	190,0
4545	190,0
5040	270,0
5050	270,0